1 前言

在前几篇文章中，有很多读者对于卷积有一些不理解，这期专门做一篇关于卷积的文章帮助大家理解。但这仅仅只是对卷积操作有了一个总体的认识，其中仍有许多细节的地方没有进行介绍。例如：

①什么是多卷积核卷积？
②卷积操作具体是怎么计算的？
③深度卷积又是怎么一回事儿？
④哪些场景下可以运用卷积操作（仅仅只是图片吗）？

因此，在接下来的这篇文章中，笔者将主要从这四个方面来继续卷积操作的工作原理。

2 什么是多卷积核

2.1 卷积

从本质上讲，卷积的计算过程其实同全连接一样，也是各个神经元之间的线性组合。只是卷积操作在进行线性组合时选择的是特定位置上的神经元。下面我们首先通过一张动图来直观感受一下卷积的过程。

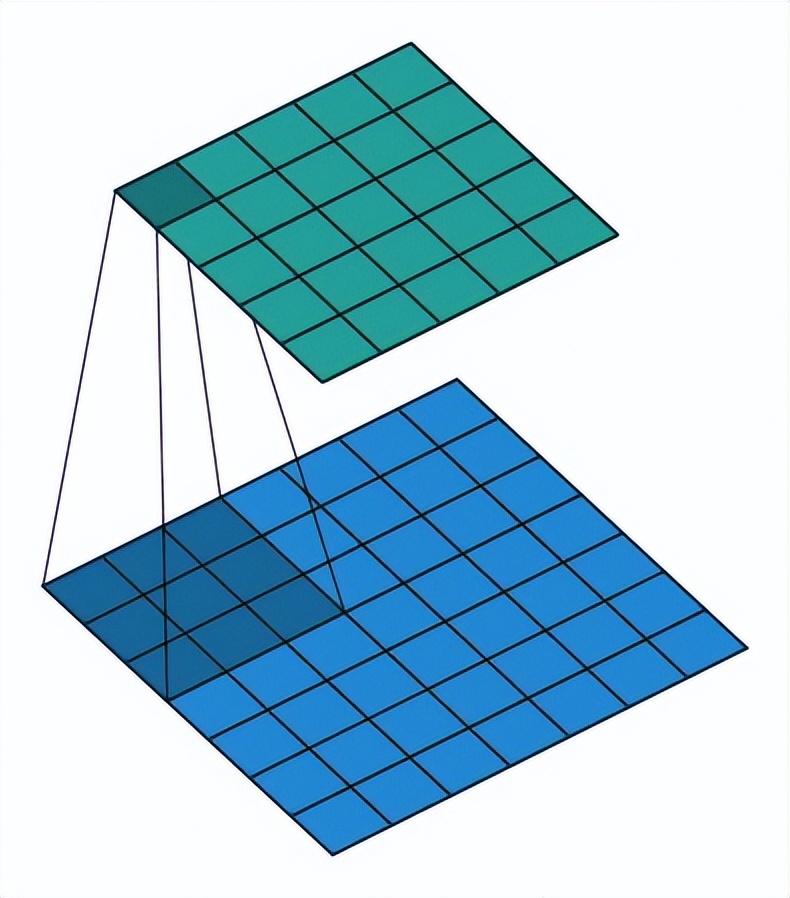
图 1. 卷积计算图

如图1所示，卷积操作其实就是每次取一个特定大小的矩阵FF（蓝色矩阵中的阴影部分），然后将其对输入XX（图中蓝色矩阵）依次扫描并进行内积的运算过程。可以看到，阴影部分每移动一个位置就会计算得到一个卷积值（绿色矩阵中的阴影部分），当FF扫描完成后就得到了整个卷积后的结果YY（绿色矩阵）。

同时，我们将这个特定大小的矩阵FF称为卷积核，即convolutional kernel或kernel或filter或detector，它可以是一个也可以是多个；将卷积后的结果YY称为特征图，即feature map，并且每一个卷积核卷积后都会得到一个对应的特征图；最后，对于输入XX的形状，都会用三个维度来进行表示，即宽（width），高（high）和通道（channel）。例如图1中输入XX的形状为[7,7,1]。

2.2 多卷积核

注意，在上面笔者提到了卷积核的个数还可以是多个，那我们为什么需要多个卷积核进行卷积呢？在上一篇文章中我们介绍到：对于一个卷积核，可以认为其具有识别某一类元素（特征）的能力；而对于一些复杂的数据来说，仅仅只是通过一类特征来进行辨识往往是不够的。因此，通常来说我们都会通过多个不同的卷积核来对输入进行特征提取得到多个特征图，然再输入到后续的网络中。

图 2. 多卷积核卷积图

如图2所示，对于同一个输入，通过两个不同的卷积核对其进行卷积特征提取，最后便能得到两个不同的特征图。从图2右边的特征图可以发现，上面的特征图在锐利度方面明显会强于下面的特征图。当然，这也是使用多卷积核进行卷积的意义，探测到多种特征属性以有利于后续的下游任务。

3 卷积的计算

到此为止， 对于卷积的原理和意义就算是交待完了，并且通过这些动态图片的展示，我们也有了更为直观的了解。但所谓数无形时少直觉，形少数时难入微。因此，下面我们就以单通道（灰度图）和三通道的输入来实际计算一下整个卷积的过程。

3.1 单通道单卷积核

如图3所示，现在有一张形状为[5,5,1]的灰度图，我们需要用图3右边的卷积核对其进行卷积处理，同时再考虑到偏置的作用。那么其计算过程是怎么样的呢？

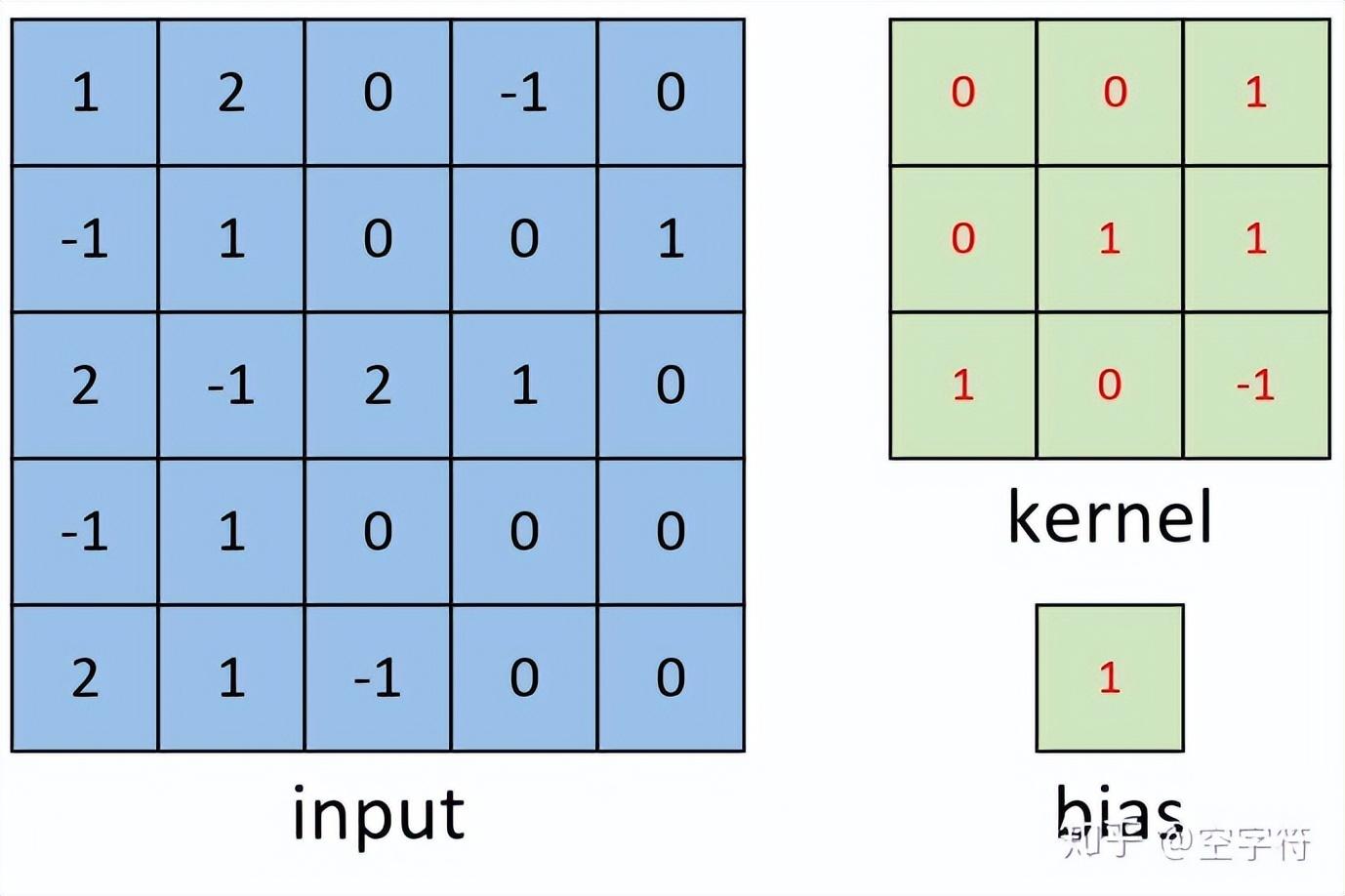
图 3. 输入与卷积

如图4所示，右边为卷积后的特征图（feature map），左边为卷积核对输入图片左上放进行卷积时的示意图。因此，对于这个部分的计算过程有：

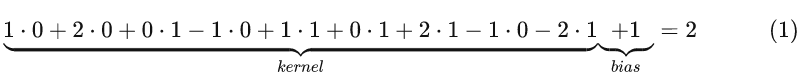
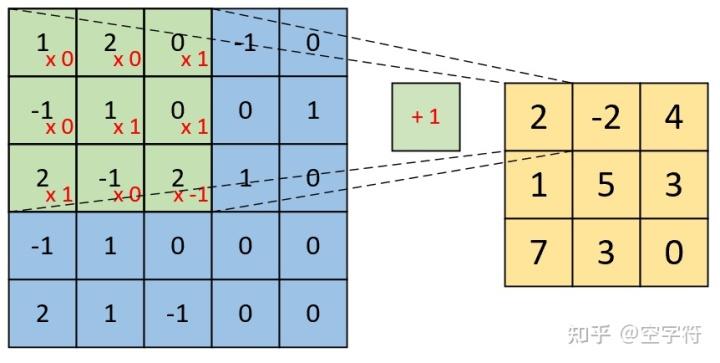
图 4. 单通道单卷积（一）

同理，对于最右下角部分卷积计算过程有：

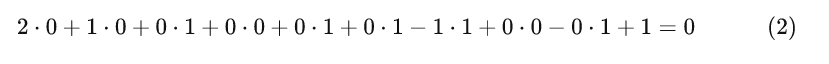
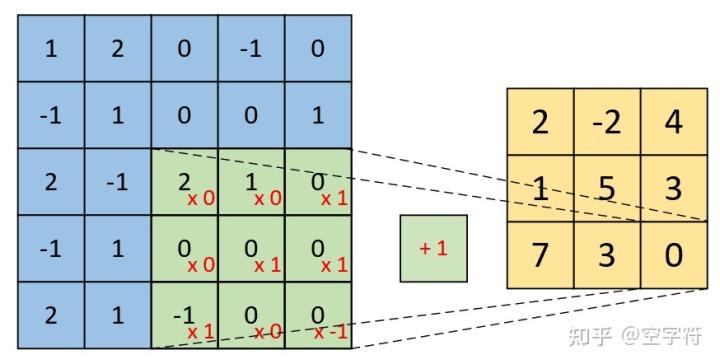
图 5. 单通道单卷积（二）

因此，对于最后卷积的结果，我们得到的将是一个如图5右边所示形状为[3,3,1]的特征图。到此我们就把单通道单卷积的计算过程介绍完了。下面我们再来看单通道多卷积核的例子。

3.2 单通道多卷积核

如图6所示，左边依旧为输入矩阵，我们现在要用右边所示的两个卷积核对其进行卷积处理。

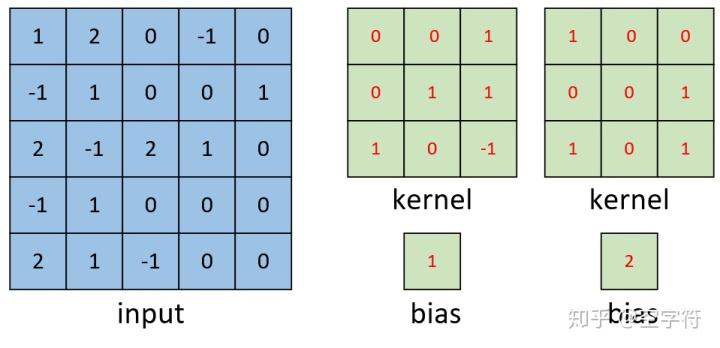
图 6. 单通道多卷积（一）

同时可以看到，图6中右边的第一个卷积核就是图3里的卷积核，其结果也就是图5中计算得到的结果。对于旁边的卷积核，其计算过程如图7所示：

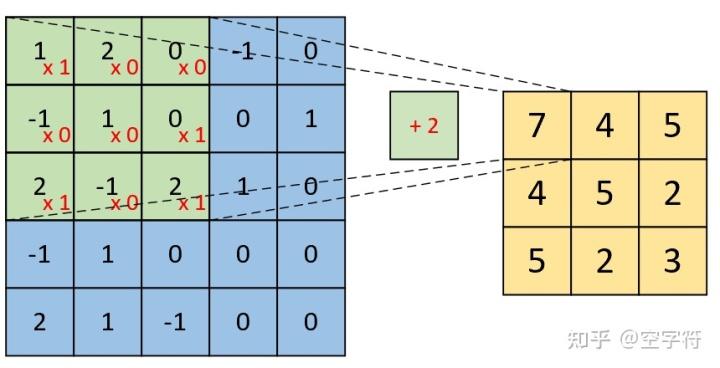
图 7. 单通道多卷积（二）

最后我们便能得到如图8右边所示的，形状为[3,3,2]的卷积特征图，其中2表示两个特征通道。

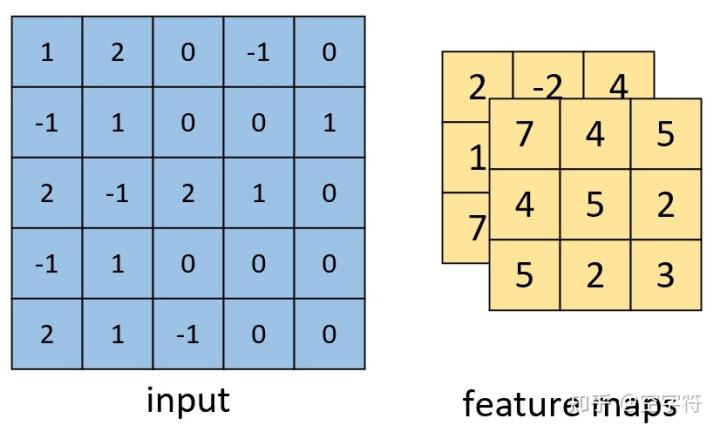
图 8. 单通道多卷积结果

到此，对于单通道的卷积计算过程就介绍完了。但通常情况下，我们遇到得更多的就是对多通道的输入进行卷积处理，例如包含有RGB三个通道的彩色图片等。接下来，笔者就开始介绍多通道的卷积计算过程。

3.3 多通道单卷积核

对于多通道的卷积过程，总体上还是还是同之前的一样，都是每次选取特定位置上的神经元进行卷积，然后依次移动直到卷积结束。下面我们先来看看多通道单卷积核的计算过程。

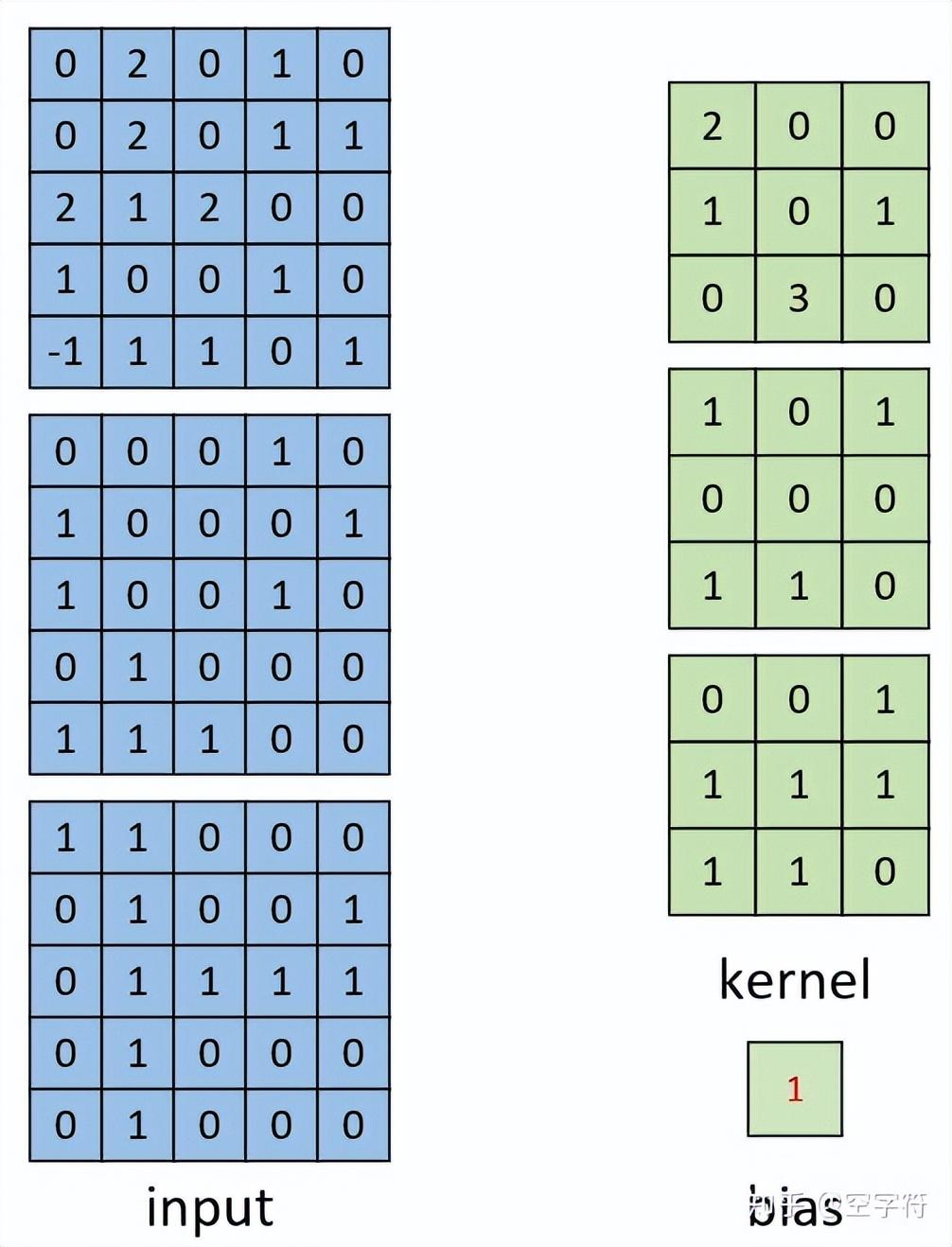
图 9. 多通道单卷积输入

如图9所示，左边为包含有三个通道的输入，右边为一个卷积核和一个偏置。注意，强调一下右边的仅仅只是一个卷积核，不是三个。笔者看到不少人在这个地方都会搞错。因为输入是三个通道，所以在进行卷积的时候，对应的每一个卷积核都必须要有三个通道才能进行卷积。下面我们就来看看具体的计算过程。

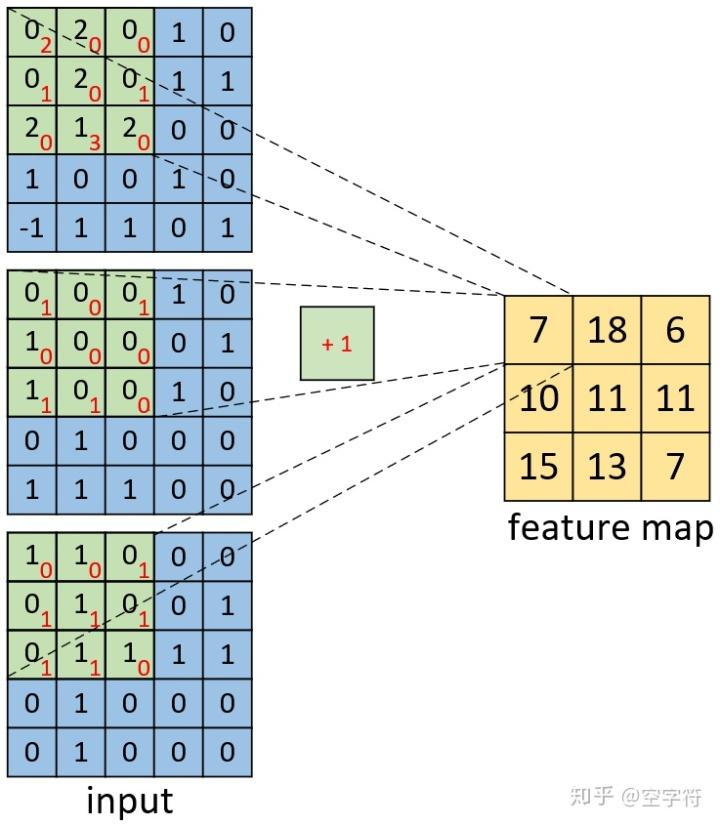
图 10. 多通道单卷积核图

如图10所示，右边为卷积后的特征图（feature map），左边为一个三通道的卷积核对输入图片左上放进行卷积时的示意图。因此，对于这个部分的计算过程有：

也类似于上述计算步骤。由此我们便能得到如图10右边所示卷积后的形状为[3,3,1]的特征图。

3.4 多通道多卷积核

在介绍完多通道单卷积核的计算过程后，我们再来看看多通道多卷积核的计算过程。

图 11. 多通道多卷积核图

如图11所示，左边依旧为输入矩阵，我们现在要用右边所示的两个卷积核对其进行卷积处理。同时可以看到，第一个卷积核就是图9中所示的卷积核，其结果如图10所示。对于第二个卷积核，其计算过程也和式子(3)(3)类似，都是将每个通道上的卷积结果进行相加，最后再加上偏置。因此，最后我们便能得到如图12右边所示的，形状为[3,3,2]的卷积特征图，其中2表示两个特征通道。

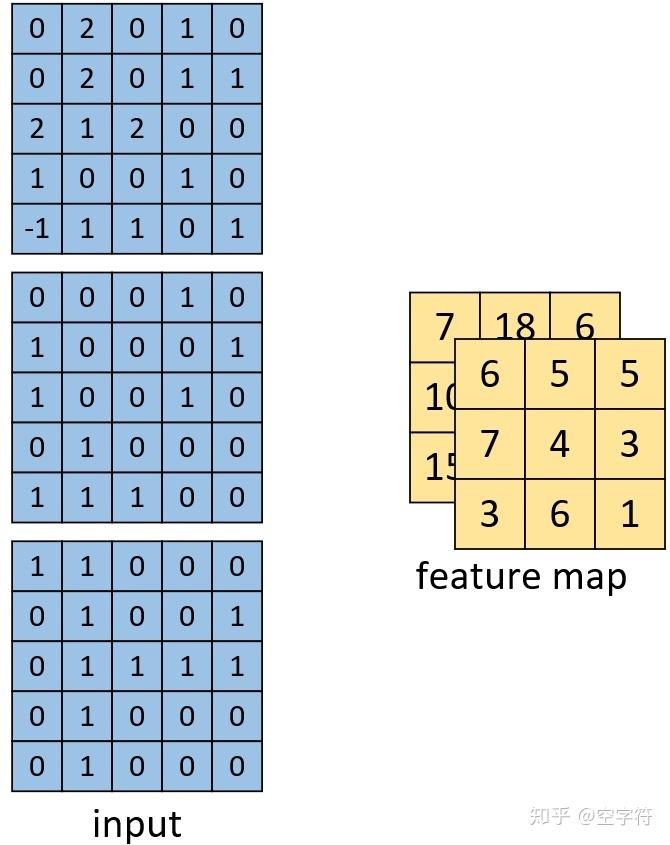
图 12. 多通道多卷积核结果图

同时，从上面单通道卷积核多通道卷积的计算过程可以发现：

（1）原始输入有多少个通道，其对应的一个卷积核就必须要有多少个通道，这样才能与输入进行匹配，也才能完成卷积操作。换句话说，如果输入数据的形状为[n,n,c]，那么对应每个卷积核的通道数也必须为c。

（2）用k个卷积核对输入进行卷积处理，那么最后得到的特征图一定就会包含有k个通道。例如，输入为[n,n,c]，且用k个卷积核对其进行卷积，则卷积核的形状必定为[w1,w2,c,k]，最终得到的特征图形状必定为[h1,h2,k]；其中w1,w2为卷积核的宽度，h1,h2为卷积后特征图的宽度。

4 深度卷积

到这里，对于多种情况下的卷积计算过程就介绍完了。接下来我们再来探索本篇文章中的最后两个问题：为什么需要深度卷积以及什么样的场景下可以使用卷积。

4.1 为什么需要深度卷积

所谓深度卷积就是卷积之后再卷积，然后再卷积。卷积的次数可以是几次，也可以是几十次、甚至可以是几百次。因此，这就带来了一个问题，为什么需要深度卷积？在前面的两篇文章（文章一、文章二）中，笔者介绍了在全连接网络中我们可以通过更深的隐藏层来获取到更高级和更抽象的特征，以此来提高下游任务的精度。因此，采用深度卷积也是处于同样的目的。

在上一篇文章中笔者介绍到，卷积操作可以看作是对上一次输入的特征提取，即用来抓取输入中是否包含有某一类的特征。但是，通常情况下，输入的图像数据都是由一系列特征横向和纵向组合叠加起来的。因此，对于同一层次（横向）的特征我们需要通过多个卷积核对输入进行特征提取；而对于不同层次（纵向）的特征我们需要通过卷积的叠加来进行特征提取。

图 13. 深度卷积图

如图13所示[1]，对于输入的一张图片，我们可以通过取多次叠加卷积后的结果来进行物体的分类任务。从图中可以发现，对于一开始的几次卷积，我们还能看到一些汽车的轮廓；但是在后续的多次叠加卷积处理后，我们人眼也就再也看不所谓汽车的影子了。但是，这些更高级的、抽象的特征却真实的能够提高模型最终的任务精度。因此，在一定的条件下，你甚至可以认为卷积的次数越多越好。在后续的文章中，笔者也会通过实验来进行对比。

4.2 什么样的场景下可以用卷积

由于大部分介绍卷积的资料都是从图像识别说起的，因此大多数对这一技术也就存在着一个固有的思维，那就是仅仅只能用于图像的特征提取。尽管卷积的由来的确是为了用于对图像数据的特征提取，但它同样能够被用于一些非图像数据的场合中。那既然如此，什么样的场景下可以使用卷积呢？

简单一句话总结起来就是，在相邻空间位置上具有依赖关系的数据均可以通过卷积操作来进行特征提取。为什么？回顾一下图像数据最重要的属性是什么？不就是相邻位置上的像素之存在着空间上的依赖（space-correlation ）关系吗？对于任意位置上的像素值来说，其周围的像素值或多或少都与其有着一定的关系，例如颜色的渐变过程。

因此，对于那些相邻空间位置存在着依赖关系的数据，我们都可以通过卷积操作来对其进行特征提取。例如网格流量数据[2]、词向量垂直堆叠而成的文本数据[3]、汽车道路构成的车速矩阵等。

5 总结

在这篇文章中，笔者首先引入了卷积中常见的五个问题；然后围绕着这五个问题依次介绍了什么是多卷积核卷积、卷积的具体计算过程、什么又是深度卷积以及什么样的场景下可以使用卷积操作等。